Keywords
Normalized solutions
Saturable nonlinearity
Pure-power nonlinearity
How to Cite
Abstract
We investigate the existence of normalized solutions to the biharmonic equation with combined pure-power and saturable nonlinearities:
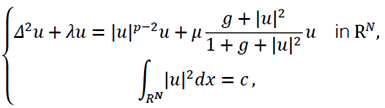
where 5 < N < 7, 2 < p < 4*: =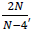 
μ > 0 is a parameter, λ ∈ R arises as a Lagrange multiplier associated with the L2-constraint, and – 1 < g < 0 is a constant. By employing variational methods and analyzing the problem on the Pohozaev manifold, we establish the existence of ground state solutions in the L2-subcritical regime and mountain-pass type solutions in the L2-supercritical regime.
References
Karpman V. Stabilization of soliton instabilities by higher order dispersion: KdV-Type Equations. Phys Lett A. 1996; 210: 77-84. https://doi.org/10.1016/0375-9601(95)00752-0
Karpman V, Shagalov A. Stability of solitons described by nonlinear Schrödinger-type equations with higher-order dispersion. Physica D. 2000; 144: 194-210. https://doi.org/10.1016/S0167-2789(00)00078-6
Han Z. Constrained minimizers of the fourth-order Schrödinger equation with saturable nonlinearity. Math Methods Appl Sci. 2024; 6488-94. https://doi.org/10.1002/mma.10685
Bellazzini J, Visciglia N. On the orbital stability for a class of nonautonomous NLS. Indiana Univ Math J. 2010; 59: 1211-30. https://doi.org/10.1512/iumj.2010.59.3907
Phan T. Blow up for biharmonic Schrödinger equation with critical nonlinearity. Z Angew Math Phys. 2018; 69: 1-11. https://doi.org/10.1007/s00033-018-0922-0
Liu J, Zhang Z. Normalized solutions to biharmonic Schrödinger equation with critical growth in RN. J Comput Appl Math. 2023; 42-276. https://doi.org/10.1007/s40314-023-02417-4
Liu J, Zhang Z, Guan Q. Existence and multiplicity of normalized solutions to biharmonic Schrödinger equations with subcritical growth. Bull Iran Math Soc. 2023; 49-80. https://doi.org/10.1007/s41980-023-00823-2
Lin T, Wang X, Wang Z. Orbital stability and energy estimate of ground states of saturable nonlinear Schrödinger equations with intensity functions in R2. J Differ Equ. 2017; 263: 2750-86. https://doi.org/10.1016/j.jde.2017.05.030
Wang X, Wang Z. Normalized multi-bump solutions for saturable Schrödinger equations. Adv Nonlinear Anal. 2020; 9: 1259-77. https://doi.org/10.1515/anona-2020-0054
Rao N, Farid M, Jha NK. A study of (σ, μ)-Stancu-Schurer as a new generalization and approximations. J Inequal Appl. 2025; article no. 104. https://doi.org/10.1186/s13660-025-03348-w
Aldosary SF, Farid M. A viscosity-based iterative method for solving split generalized equilibrium and fixed point problems of strict pseudo-contractions. AIMS Math. 2025; 10(4): 8753-76. https://doi.org/10.3934/math.2025401
Rao N, Farid M, Jha NK. Approximation properties of a fractional integral-type Szász-Kantorovich-Stancu-Schurer operator via Charlier polynomials. Mathematics. 2025; 13: 3039. https://doi.org/10.3390/math13183039
Fernández A, Jeanjean L, Mandel R. Non-homogeneous Gagliardo-Nirenberg inequalities in RN and application to a biharmonic non-linear Schrödinger equation. J Differ Equ. 2022; 330: 1-65. https://doi.org/10.1016/j.jde.2022.04.037
Wang H. Palais-Smale approaches to semilinear elliptic equations in unbounded domains. Electron J Differ Equ Monograph. 2004; 06: 142. https://doi.org/10.58997/ejde.mon.06
Mederski J, Siemianowski J. Biharmonic nonlinear scalar field equations. Int Math Res Not. 2023; 19963-65. https://doi.org/10.1093/imrn/rnac303
Soave N. Normalized ground states for the NLS equation with combined nonlinearities. J Differ Equ. 2020; 269: 6941-87. https://doi.org/10.1016/j.jde.2020.05.016
Ghoussoub N. Duality and perturbation methods in critical point theory. Cambridge: Cambridge Univ Press; 1993. https://doi.org/10.1017/CBO9780511551703
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright (c) 2025 Yue Ma, Ziheng Zhang